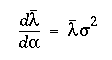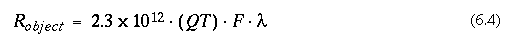Oke system magnitude at the corrected mean wavelength of the filter:

where Snu is the flux in ergs cm-2 s-1 Hz-1 as in Oke and Gunn, Ap. J., 266, 713 (1983) at the effective mean wavelength of the filter  . It can be shown that
. It can be shown that
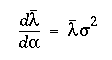
if the integrands are weighted by a source with spectral index a in the definition of lambda. See also Koornneef, J., et al. "Synthetic Photometry and the Calibration of the Hubble Space Telescope" in Highlights of Astronomy (7, 833, J.-P. Swings Ed (1983). Combining the above equations gives

6.3.3 Count Rates for Emission Line Sources
The count rate in units of e- s-1 for a monochromatic emission line is given by
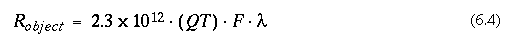
where F is the emission line flux in units of ergs cm-2 s-1, and lambda is the wavelength of the line in Angstroms. The quantity QT is the (system + filter) quantum efficiency at the wavelength of the line, which can be determined from inspection of the figures in section A.2, "Passbands including the System Response", on page 211. For lines near the maxima of the filter transmission curves, it should be sufficient to use QTmax from Table 6.1
. Note that the integrated filter efficiency is not relevant for the signal calculation.
In cases where the width of the line approaches that of the filter, it will be necessary to convolve the line shape and filter bandpass using either the SYNPHOT or XCAL programs.
For example, Ha emission at 6563Å, with total source flux F=10-16 erg s-1 cm-2, observed through the F656N filter (total system throughput T=0.104 from "F656N, F658N, F673N, F675W, F702W, F785LP" on page 217), will produce a target count rate Robject=0.155 e- s-1 integrated over the entire source.
- 6.3.1 - Count Rates for Stellar Sources
-
- 6.3.2 - Count Rates for Power Law Sources
-
- 6.3.3 - Count Rates for Emission Line Sources
-









 . It can be shown that
. It can be shown that