Science with the Hubble Space Telescope -- II
Book Editors: P. Benvenuti, F. D. Macchetto, and E. J. Schreier
Electronic Editor: H. Payne
Hans-Martin Adorf
Space Telescope -- European Coordinating Facility,
European Southern Observatory,
Karl-Schwarzschild-Straße 2,
D-85748 Garching b. München,
F.R. Germany,
Phone: +49-89-320 06-261,
Internet: adorf@eso.org
Abstract:
The Cramér-Rao theorem of advanced statistics is used to predict a
rigorous bound to the precision with which photometry and astrometry
can be carried out with data from the Wide Field and Planetary
Camera 2. The specific question addressed is how subpixel dithering influences
photometry and astrometry. Progress on a maximum-likelihood image
registration algorithm is reported, which in the future may become a
commendable tool for high-precision astrometric programs. Finally
the properties of a statistically optimum, unbiased, linear
photometric algorithm are described; this method reduces photometric errors
in the presence of significant pixel-to-pixel quantum efficiency
variations as may be expected for NICMOS-type detector arrays.
Keywords: astrometry, models, photometry, statistical errors
``It can be shown
that a statistically sound estimation
of scientific parameters
requires [...] a complete physical understanding
of the instrumental detection chain.''
---M. Rosa, 1995
Photon shot noise due to the quantum nature of light introduces
inevitable statistical errors into the data obtainable from the
present and future cameras on-board the Hubble Space Telescope. Two
questions naturally arise: firstly, how big are these errors; and,
secondly, what can be done (i.e., which data analysis algorithms
should be used) in order to minimize resulting errors?
In the following we shall see how the first of these questions can be
comprehensively answered with the help of the remarkable Cramér-Rao
theorem of advanced statistics which, when applied to imagery with
array detectors, enables us to predict lower bounds to the errors in
flux and position measurements of point sources as a function of both
the object brightness and its exact sub-pixel position.
With respect to the second question progress is reported in two areas,
namely (1) the development of a maximum-likelihood astrometric
algorithm for optimum ``centroiding'' of noisy images in the presence
of undersampling---a problem plaguing both WFPC2 and NICMOS---and
(2) an optimized linear flux estimator which minimizes the statistical
errors in the presence of considerable spatial variations in the
detector's quantum efficiency map (``flat field'') as is typical for
NICMOS-type detectors.
The study of all these questions requires a stochastic model of the
observational process. This is in line with the remark by Rieke et al.
(1993) that ``To extract scientifically useful data from these [NICMOS]
images will require a complete understanding of the arrays used to produce
the images.''
The observational technique of point source photometry with WFPC2 is
fairly well established by now. Nevertheless there are remaining
questions concerning the use of large- and small-scale dithering (see
below) which so far have not yet been fully settled. In particular,
geometric distortion requires considerable attention when images are
taken with large dithers, as in case of the Hubble Deep Field
(Williams et al. 1996, this conference).
On the other hand, it appears that WFPC2 has not been used very much
for specific astrometric programs. This situation appears to be
changing rapidly: the number of astrometric observing proposals
planning to use WFPC2 has considerably increased in the present cycle
(Stanley, priv. comm.), and while several groups are working
towards astrometric programs, astrometry is emerging as an important
observational technique for WFPC2.
Consider, for instance, the problem of a proper motion study of the thin
disk, thick disk, and halo Galaxy components. High astrometric
precision is required in order to distinguish a prograde from a
retrograde halo motion. The sample mean RMS error must be smaller than
0.6 mas/year (Mendez 1995, priv. comm.) which for a baseline of 1
year and a typical sample size of say 180 stars in the range
17 < V < 19 mag requires an RMS error for an individual star of less
than 6 mas on average. Recall that a WFC2 pixel has a projected
diameter of 100 mas.
It has been predicted (Adorf 1996b) that such an astrometric precision
should indeed be achievable with WFPC2---even for fainter stars.
These predictions make use of the already mentioned Cramér-Rao
minimum variance bound (MVB) theorem of advanced statistics (Kendall
& Stuart 1979) which allows one to compute a rigorous lower bound to
the RMS error for an unbiased estimator of a physical quantity. This
theorem, independently discovered by several statisticians, has
occasionally appeared in the astronomical literature (e.g., Jakobsen
et al. 1992, for further refs. see Adorf 1996c), but its
importance is not widely recognized, despite the fact that it has
several strong points: the specified bound is not too difficult to
compute; it is independent of any particular data analysis method; and
the theorem is applicable to the otherwise difficult multivariate
parameter case.
In an extension to previous work (Adorf 1996b), the Cramér-Rao
theorem is used here to study the effects an observing strategy, using
sub-pixel dithering, may have on photometry and astrometry.
In view of the fact that the WFC2 undersamples the optical point
spread function, there has been a long-standing interest not only in
the question how well one can carry out point source photometry and
astrometry on single frames (or stacks of frames with the same
telescope pointing), but also whether sub-pixel dithering and image
combination may actually help to improve the precision.
Two observing strategies are being compared: (a) four WFC2 frames of
1000 sec exposure time each, taken with the same telescope
pointing (a standard single-pointing stack); (b) four WFC2 frames of
1000 sec exposure time each, taken with 1/2 WFC2 pixels offsets in
both directions (the regular 'quartet' frame strategy, Adorf 1995).
MVB calculations have been carried out comparing these two
observational data sets. They have led to the following preliminary
conclusions which are reported here without proof (see Fig. 1):
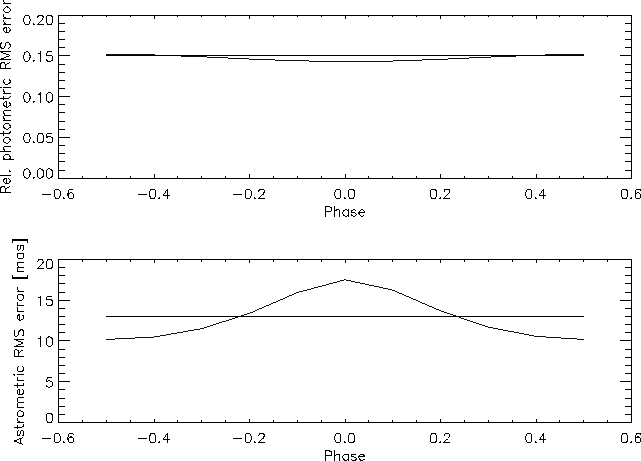
Figure: The influence of object-pixel phase on photometric and
astrometric errors, computed for a total of four 1000 sec exposures of
an V = 27 mag A-star observed with 5 mas jitter. The top panel shows
the minimum variance bound to the relative photometric error for
four frames observed according to the quartet dither strategy
(horizontal line) and for a stack of four frames observed with the
same pointing (curved line). The bottom panel shows the minimum
variance bound to the astrometric error, again for a quartet
dither strategy (horizontal line) and for a single pointing stack of
four frames (curved line).
The pixel center has phase =0, its edges have phase 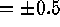
1. For photometry of an isolated point source, it practically makes no
difference whether one is using a regularly dithered frame quartet,
or simply a single-pointing frame stack.
2. For astrometry of a single point source, using a dithered frame
quartet does make a difference. With dithered frames one can attain
the same (bound to the) astrometric precision independent of the
object-pixel phase. With a stack of single pointing data, however the
(bound to the) astrometric precision varies with object-pixel phase
by a factor of up to about 2. The variations are more pronounced for
fainter objects and less so for brighter objects.
3. For astrometry of an ensemble of objects it seems that it does not
really make a difference which observing strategy is used, since some
objects will fall close to pixel boundaries and therefore will be
locatable with higher precision, and others will fall closer to pixel
centers, and will have a higher positional errors. On average these
effects are expected to largely cancel out, although a more refined
study covering all dither positions across the 2D area of
a pixel are necessary to settle this question quantitatively.
4. In the presence of critical or insufficient sampling it is important
to understand the precise shape of the wavelength dependent pixel
response function (cf. Jorden et al. 1993, 1994, Adorf 1995).
The results of these calculations may be used in two ways: firstly,
for precision goals are set which should be approached as much as
possible by real-world data analysis algorithms; secondly, the (bound
to the) error of a position measurement, as a function of object
magnitude and object-pixel phase, can be used for computing a
statistical weight in an astrometric solution involving several
objects.
We now turn to the question about optimized data analysis algorithms.
We consider the problem of carrying out good astrometry in the presence
of critical or insufficient sampling and Poisson noise.
In typical astronomical scenes, the objects for which astrometry shall
be obtained may span a high dynamic range. However, since most objects
are usually faint, any astrometric algorithm must not only cope with
faint (noisy) objects, but actually be optimum for such objects. The
question therefore arises how to measure the positions of stars (and
also galaxies) with minimum statistical errors to subpixel precision
(cf. Welch 1993).
To this end a maximum likelihood image ``centroiding'' algorithm has
been devised (Fig. 2) which is model-based and statistically
optimized in the sense that it uses all available positional
information. In fact, the algorithm is not restricted to point
sources, but may also work with extended sources, as long as there is
a sufficiently sampled model of the light distribution. Such a model
can often be constructed a posteriori from the data. The fact that the
algorithm can work with an arbitrary light distribution entails the
possibility to fit the position of a set of stars (and galaxies)
simultaneously---and automatically with the appropriate statistical
weights.

Figure: Flow chart of the iterative maximum-likelihood image
``centroiding'' algorithm. In addition to the data, the algorithm
requires a sufficiently sampled model of the object light
distribution, which may be constructed from the data. The
implementation of the algorithm internally makes use of certain high
fidelity image processing operators for lossless image shift and
rotation, and for computing spatial derivatives.
The same algorithm can also be used for precision registration of
shifted and rotated WFPC2 frames; this is the purpose for which it had
originally been conceived. Another potential application is that of
automatic registration of HST and ground-based frames, which will
become more important in the future.
The Near Infrared Camera and Multi-Object Spectrometer (NICMOS)
instrument (Thompson 1995, Axon et al. 1995) is one of the
second-generation instruments to be installed on HST during the 1997
refurbishment mission. It is anticipated that in many respects imagery
with NICMOS will resemble that with WFPC2, although the undersampling
problem is somewhat less severe for NICMOS. However, there
are two noticeable differences: first, as is known from the ground,
the quantum efficiency (QE) map of NICMOS-detector arrays usually
displays non-negligible spatial variations which are also
color-dependent. Secondly, infrared observations encounter
considerable background.
Fortunately, as long as the QE-variations can be accurately and
precisely calibrated, there is no reason for excessive worries. Using
a stochastic model of the NICMOS detector array, an optimized,
unbiased, linear photometric algorithm can easily be constructed which
weighs the contributions from the different pixels according to their
inverse variance.
The following conclusions are noted without proof:
(1) There is no better unbiased linear photometric algorithm (capable
of carrying out photometry with lower variance).
(2) The inverse variance of the object flux estimate is the sum of
the inverse variances of the (background-subtracted) ``scaled'' counts
at the individual pixels.
(3) At least for an isolated point source, the optimum linear
estimator for photometry is an MVB-estimator, i.e., it attains the
Cramér-Rao minimum variance bound (MVB). Therefore the maximum
likelihood estimator for photometry also attains the MVB, and is as
efficient (but not superior to) the optimum linear estimator. In other
words, to the extent precision photometry is possible, it will be
delivered by the linear algorithm using the optimum statistical
weights.
Widely used photometric algorithms such as DAOPHOT currently only work
on calibrated data. In order to optimism these algorithms for
photometry using data from NICMOS-type detectors, it would be
advantageous to modify them so that they may accept quantum efficiency
maps as secondary input.
It has been pointed out by Rieke et al. (1993) that
``Astronomical use of these [NICMOS] arrays [...] involves extracting
accurate photometric information and detection of sources in spite of
high background levels.'' Clearly, the higher the background (noise)
the more important it becomes to use efficient data analysis
procedures (``estimators'') in order to exploit all the information in
the data.
Current photometric algorithms usually estimate the background only
outside of the object image. However, when the background level is
high compared to the object flux, there is considerable information
about the background in the same pixels that contain the object image!
Indeed, the Fisher information (Kendall & Stuart 1979) about the
background level in a given pixel is simply the inverse of the
variance (= expected counts) in that pixel. Thus, for high background
levels the information about the background level within the object
image is almost as high as outside.
This points to the necessity of upgrading existing photometric
software so that it takes advantage of all available background
information.
Let us finish with some general conclusions resulting in part
from on-going work. The detailed assumptions and derivations
supporting the claims below are beyond the scope of this contribution,
and will be the subject of a forthcoming paper (Adorf 1996c).
(1) Optimized data analysis algorithms (statistical ``estimators'')
require the calibration data (e.g., the quantum efficiency/flat field
map) as secondary input.
(2) An optimized photometric estimator may benefit from undoing the previous
flat-fielding calibration, which introduces suboptimal statistical weights.
(3) The Fisher information at each pixel provides a good means for
developing an intuition about where how much of the information about
the parameter of interest resides.
(4) The experience with the undersampling of the WFPC2 camera suggests that
it would be useful to calibrate the NICMOS pixel response function via
ground-based measurements. Similarly, the experience with the
geometric distortions of the WFPC2 camera points out the necessity to
characterize potential geometric distortions of the NICMOS camera via
measurements and/or ray-tracing model calculations.
(5) It is important to have an agreed-upon stochastic model for WFPC2
and NICMOS. Using a stochastic model allows one to study the precision
limits for photometry and astrometry. Moreover, optimized data
analysis algorithms can be derived.
Finally, there is an urgent need for a NICMOS exposure time calculator
similar to that for the WFPC2 (Adorf et al. 1996), in
order to have a reliable means for predicting object and background
counts. The latter are needed as input for theoretical statistical
calculations, e.g., those concerning bounds to the precision of
photometry and astrometry, and in order to facilitate the quantitative
assessment of advanced statistical data analysis algorithms.
Acknowledgments:
Many thanks are due to Rene Mendez (ESO) for numerous suggestions. I
should also like to thank John Biretta, Andy Fruchter, Barry Lasker,
Peggy Stanley and Anatoly Suchkov (STScI), Dave Clements, Guido De
Marchi, and Dante Minitti (ESO), as well as my colleagues Richard Hook
and Jeremy Walsh (ST-ECF) for useful discussions.
References:
Adorf, H.-M. 1995, ``WFPC2 observations---when and how to
dither?'', ST-ECF Newslett., 23, 19
Adorf, H.-M. 1996a, ``High-fidelity image processing
operators'', in preparation
Adorf, H.-M. 1996b, ``Limits to the Precision of Joint
Flux- and Position-Measurements'', in Astronomical Data
Analysis Software and Systems V, ASP Conf. Ser., eds. J. Barnes & G.
Jacoby (San Francisco, ASP), in press
Adorf, H.-M. 1996c, ``Minimum errors in joint photometric
and astrometric measurements'' or ``What the Cramér-Rao minimum
variance bound can tell us'', in preparation
Adorf, H.-M., Biretta, J., & Suchkov, A. 1996, ``The WFPC2
exposure time calculator'', ST-ECF Newsl., in preparation
Axon, D., Bushouse, H., MacKenty, J., & Skinner, C. 1995,
``Near Infrared Camera and Multi-Object Spectrometer Instrument
Mini-Handbook'', in New Instruments for Second Servicing
Mission, Space Telescope Science Institute, Servicing Mission Office,
Baltimore, p. 3
Jakobsen, P., Greenfield, P., & Jedrzejewski, R. 1992, ``The
Cramér-Rao lower bound and stellar photometry with aberrated HST
images'', A&A, 253, 1, 329--332
Jorden, P., Deltorn, J.-M., & Oates, P. 1993, ``The
Innermost Secrets of CCDs'', Greenwich Observatory Newsletter,
41, 9/93, 1
Jorden, P.R., Deltorn, J.-M., & Oates, A.P. 1994, ``The
non-uniformity of CCDs and the effects of spatial undersampling'', in
Proc. Instrumentation in Astronomy VIII, SPIE Vol. 2198, 13-14
March 1994, Kona, Hawaii, eds. D.L. Crawford and E.R. Craine,
(Bellingham, WA, SPIE), p. 836
Kendall, M. & Stuart, A. 1979, ``The Advanced Theory of
Statistics'', Charles Griffin & Co. Ltd., London & High Wycombe, p. 748
Rieke, M.J., Winters, G.S., Cadien, J., & Rasche, R. 1993,
in: ``Infrared Detectors and Instrumentation'', ed. A.M. Fowler,
Proc. SPIE, 1946, p. 214
Thompson, R.I. 1995, ``Scientist's Guide to NICMOS'', p. 91
Welch, S.S. 1993, ``Effects of window size and shape on
accuracy of subpixel estimation of target images'', Technical Paper,
3331 (1993), NASA
payne@stsci.edu