J.-F. Claeskens
Institut d'Astrophysique de Liège, 5, Avenue de Cointe, B-4000
Liège, Belgium
J. Surdej
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218
USA
Research Assistant, Belgian Fund for Scientific Research (FNRS) Member of the Astrophysics Division, Space Science Department of the European Space Agency; also Research Director, Belgian Fund for Scientific Research (FNRS)
has
to be smaller than 0.01 in the mass range 
--
. This
presently constitutes the best constraint on 
. Simulations show that
a careful analysis of 500 new observations of HLQs acquired with the
refurbished HST would allow us to extend the present constraint down to
, and to rule out a Universe closed by any kind of compact
objects in the mass range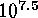 
--
.
Keywords: Gravitational Lensing - Dark Matter - Quasars
Identifying the real nature of dark matter in the Universe constitutes one of
the most challenging goals in modern astrophysics (see Carr 1990 for a
review).
Gravitational lensing provides a very powerful tool to detect the various
signatures of baryonic dark matter. Indeed, the distribution of dark matter
associated with clusters of galaxies can be probed from the detailed analysis
of giant luminous arcs and of the shear deformations of background sources
(Fort & Mellier 1994); the effect of local compact dark matter,
belonging to the disk or to the halo of our galaxy, can be detected in
micro-lensing experiments such those being presently conducted by the DUO,
EROS, MACHO and OGLE teams (see the recent review by Paczynski 1995).
Finally, the
cosmological density of isolated dark compact objects can be indirectly
constrained by
the (non) observation of `micro-lensing induced' flux variations in background
QSOs or by the (non) detection of multiply imaged sources in a flux limited
sample of QSOs. The first technique is specially sensitive to the effects of
compact objects in the mass range 
--
(Canizares 1982,
Schneider 1993).
The second technique consists in trying
to resolve multiple macro-lensed QSO images using ground-based, radio
telescopes and/or the HST with adequate high angular resolution imaging
instruments. This class of techniques has a good sensitivity in the mass range
--
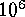, depending on the instrument being used. The
limits of this method are dictated by both the angular resolution and
the dynamics of the instrument. Using the point-mass lens model, we show in
this paper how statistical constraints can presently be derived in the above
mass range; the contribution due to HST is emphasized. To be complete, let us
mention here that by modelling the observed frequency of mutiply imaged Highly
Luminous Quasars with galaxy lenses (some examples are well known), it
has been possible to constrain the values of galactic parameters, the number
counts of QSOs and the cosmological constant (Claeskens et al. 1995a).
In the next section, we present and discuss the expression of the probability for observing doubly imaged QSOs lensed by compact objects; we also emphasize the influence of the instrumental characteristics (angular resolution and dynamics). We present the data in section 3. The results and a discussion are given in section 4.
The generic expression for the probability of observing a lensing event along
the line-of-sight to a QSO at redshift 
, due to a population of compact
objects with mass 
, uniformly distributed in space, is:
where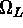 
represents the cosmological density of compact objects with
mass 
, in units of the present closure density of the Universe. Of
course, the probability P increases with 
. In the
above equation,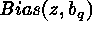 
is the so called magnification bias: because
macro-lensing amplifies the flux of a background source, observing
bright sources enhances the chance to discover a lens in a flux limited
sample of quasars. Because of these two latter effects, the probability to
discover a new lens is of course optimal when observing HLQs (typically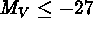 
; see Turner 1984 & Surdej et al. 1988).
Finally, 
in Eq. (1) represents the lensing
cross-section for a compact object with mass 
at redshift z to produce
double images from a QSO at redshift 
, and be detected by the given
instrument.
At a given redshift, the general cross-section for multiple imaging is a ring whose thickness depends on three competing criteria:
between lensed images
increases with the degree of misalignment between the source, the lens and
the observer, and because 
must be larger than the angular
resolution of the instrument, the angular distance between the lens and the
source, measured at the observer, must be larger than a lower limit
.
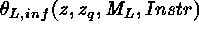between double lensed images also
increases with the degree of misalignment 
between the source, the
lens and the observer; therefore, the finite dynamics of the instrument
implies an upper limit on the angular distance 
between the lens and the source. So, the higher the dynamics of
the instrument, the larger the cross-section for lensing. 
increases
faster with 
when 
gets smaller, so, if 
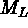is too small,
then 
: the instrument is unable to resolve
the lensed images.
must be smaller than
. So 
has to be smaller than an upper limit
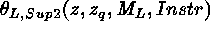. This condition sets an upper limit
(
) on the mass range of the compact objects which can be
probed.
The general expression for the lensing cross-section is the following:
where 
is the angular distance between the observer and the deflector.
More formal details on this expression for the lensing probability can be
found in Surdej et al. (1993a).
Figure 1a displays the relation existing between the dynamics and the angular
resolution (the Angular Selection Function (ASF)) for typical good seeing
observations obtained with a ground-based telescope (dotted line) and for the
pre- and post-refurbished HST (dashed and continuous lines). In some way,
these curves represent the joined performance of the instrument and of the
method of image analysis for resolving multiple images. The latter method
usually consists in carefully subtracting
a scaled PSF from the QSO image (see Surdej et al. 1995, Remy 1996). The thick
vertical line represents the maximal angular separation between the images
(criterion 3). Figure 1b
illustrates the corresponding lensing probability versus the angular
separation between the lensed images, for two different compact lens masses
(heavy lines: 
; light lines: 
). The
optical depth is expressed in 
units. The better efficiency of HST
to constrain the density of compact objects with 
is
clearly seen from Fig. 1b.
Figure: a) The ASF b) The lensing probability (see text).
Table 1: Characteristics of HST and ground based imagery surveys of HLQs (1-
Maoz et al. 1993, 2- Surdej et al. 1993a, 3- Crampton et al. 1992, 4- Yee et
al. 1993, 5- Jaunsen et al. 1995)
The present sample contains 1680 observations of 1207 different HLQs. It has been compiled by merging the HST snapshot survey (before refurbishment) and four selected ground-based imagery surveys of HLQs. Table 1 summarizes the properties of each subsample. In the case of multiple observations of a same QSO, the most efficient one has been kept. But this choice depends on the assumed lens mass. The two last columns of Table 1 show how many observations per sample have been kept, for two different lens masses. The percentages represent the internal efficiency of each subsample.
The sample presented in Table 1 only contains three lens candidates which satisfy
the hypothesis of being possibly lensed by a dark compact object (i.e., two
lensed images and no already detected galaxy-type lens) and which present an
angular separation between their images smaller than 
. These are
Q1208+1011 (Magain et al. 1992, Maoz et al. 1992), Q1009-025 (Surdej et al.
1993b) and J03.13 (Claeskens et al. 1995b).
Figure: Upper limit on 
versus 
(with a 99.7 % confidence
level).
Comparing the observed and the predicted numbers of lenses in the sample, a
firm upper limit on 
can be derived. With a 99.7% confidence level,
and adopting an Einstein-de Sitter Universe (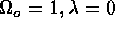
),
we find that 
in the mass range 
--
. The strongest constraint we have derived is 
for 
compact objects. The use of other cosmological models or
the identification of a yet unseen
galaxy-type lens among the three candidates would reinforce the present constraints. As shown in Fig. 2, our results are the most constraining ones
for masses larger than 
, and a closure density of the
Universe by any kind of compact objects in the mass range 
--
is ruled out.
The dotted line in Fig. 2 corresponds to a simulation of the constraints on
if 500 additional observations of HLQs were obtained with the
(presently refurbished) HST. This would drastically improve the constraint on
in the mass range 
--
. This would even
surpass the best presently existing constraints derived from VLBI radio
observations for compact objects more massive than 
(Kassiola
et al. 1991). It is
also important to note that the number counts of QSOs at radio wavelength is
not known very accurately. So, the magnification bias for radio observations
cannot be properly estimated and this makes optical observations presently
more reliable in order to derive statistical values for the cosmological
parameters. Therefore, HST can play a very important role in further
constraining the cosmological density of compact dark matter. This goal could
be achieved by carrying out a new snapshot survey.
This research has been supported by the PRODEX project for Gravitational Lens studies at the ``Institut d'Astrophysique de l'Université de Liège''.
Canizares, C.R. 1982, ApJ, 263, 508
Carr, B.J. 1990, Comments Astrophys., 14, 257
Claeskens, J.-F., Jaunsen, A., & Surdej, J. 1995a, To appear in proc. IAU 173 symposium
Claeskens, J.-F., Surdej, J., & Remy, M. 1995b, To appear in proc. IAU 173 symposium
Crampton, D., McClure, R., & Fletcher, J. 1992, ApJ, 392, 23
Fort, B. & Mellier, Y. 1994, ARA&A, 5, 239
Jaunsen, A.O., Jablonski, M., Pettersen, B.R., & Stabell, R. 1995, A&A, in press
Kassiola, A., Kovner, I. & Blandford, R. 1991 ApJ, 381, 6
Magain, P., Surdej, J., Vanderriest, C. et al. 1992, A&A, 253, L13 (Erratum: 1993, A&A, 272, 383)
Maoz, D., Bahcall, J. N., Schneider, D. P., Doxsey, R. et al. 1992, ApJ, 386, L1
Maoz, D., Bahcall, J. N., Schneider, D. P., Bahcall, N. A. et al. 1993, ApJ, 409, 28
Paczynski, B. 1995, To appear in proc. IAU 173 symposium
Remy, M. 1996, Ph.D. Thesis (Université de Liège)
Schneider, P. 1993, A&A 279, 1
Surdej, J., Magain, P., Swings, J.P. et al. 1988, Proc. of the first D.A.E.C. Workshop Large Scale Structures: Observations and Instrumentations, Paris, eds. C. Balkowski & S. Gordon
Surdej, J. et al. 1993a, AJ 105, 2064
Surdej, J., Remy, M., Smette, A. et al. 1993b, in the Proc. of the 31st Liège Int. Astroph. Coll. Gravitational Lenses in the Universe, eds. J. Surdej, D. Fraipont-Caro, E. Gosset, S. Refsdal, & M. Remy, pp 153--160
Surdej, J., Jaunsen, A., Claeskens, J.-F. et al. 1995, To appear in proc. IAU 173 symposium
Turner, E.L., Ostriker, J.P., & Gott III J.R. 1984, ApJ, 284, 1
Yee, H., Filippenko, A., & Tang, D: 1993, AJ, 105(1), 7