Strange Attractors
Edward Lorenz's first weather model exhibited chaotic behavior, but it involved a set of 12 nonlinear differential equations. Lorenz decided to look for complex behavior in an even simpler set of equations, and was led to the phenomenon of rolling fluid convection. The physical model is simple: place a gas in a solid rectangular box with a heat source on the bottom.
Lorenz simplified a few fluid dynamics equations (called the Navier-Stokes equations) and ended up with a set of three nonlinear equations:

where P is the Prandtl number representing the ratio of the fluid viscosity to its thermal conductivity, R represents the difference in temperature between the top and bottom of the system, and B is the ratio of the width to height of the box used to hold the system. The values Lorenz used are P = 10, R = 28, B = 8/3.
On the surface these three equations seem simple to solve. However, they represent an extremely complicated dynamical system. If one plots the results in three dimensions the following figure, called the Lorenz attractor, is obtained.

Projections of this attractor in the y-z and x-z two-dimensional planes are as follows:


The Lorenz attractor is an example of a strange attractor. Strange attractors are unique from other phase-space attractors in that one does not know exactly where on the attractor the system will be. Two points on the attractor that are near each other at one time will be arbitrarily far apart at later times. The only restriction is that the state of system remain on the attractor. Strange attractors are also unique in that they never close on themselves — the motion of the system never repeats (non-periodic). The motion we are describing on these strange attractors is what we mean by chaotic behavior.
The Lorenz attractor was the first strange attractor, but there are many systems of equations that give rise to chaotic dynamics. Examples of other strange attractors include the Rössler and Hénon attractors.
The Rössler attractor arose from studying oscillations in chemical reactions. It is formed from another set of Navier-Stokes equations, namely:
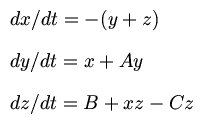
where A = 0.2, B = 0.2, and C = 5.7. A projection in the x-y plane of this attractor is:

Another strange attractor, created recursively, is the Hénon attractor:

