Logistic Equation
One often looks toward physical systems to find chaos, but it also exhibits itself in biology. Biologists had been studying the variability in populations of various species and they found an equation that predicted animal populations reasonably well. This equation was a simple quadratic equation called the logistic difference equation. On the surface, one would not expect this equation to provide the fantastically complex and chaotic behavior that it exhibits.
The logistic difference equation is given by
where r is the so-called driving parameter. The equation is used in the following manner. Start with a fixed value of the driving parameter, r, and an initial value of x0. One then runs the equation recursively, obtaining x1, x2, . . .xn. For low values of r, xn (as n goes to infinity) eventually converges to a single number. In biology, this number (xn as n approaches infinity) represents the population of the species.
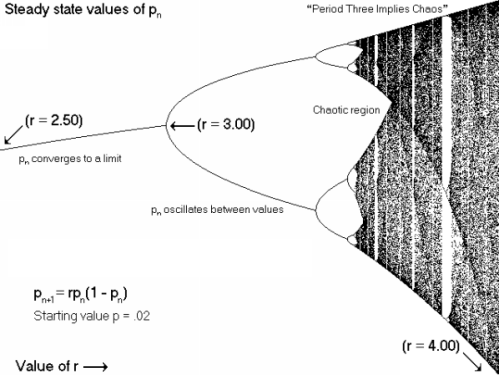
It is when the driving parameter, r, is slowly turned up that interesting things happen. When r = 3.0, xn no longer converges — it oscillates between two values. This characteristic change in behavior is called a bifurcation. Turn up the driving parameter even further and xn oscillates between not two, but four values. As one continues to increase the driving parameter, xn goes through bifurcations of period eight, then sixteen, then chaos! When the value of the driving parameter r equals 3.57, xn neither converges or oscillates — its value becomes completely random. For values of r larger than 3.57, the behavior is largely chaotic. However, there is a particular value of r where the sequence again oscillates with period of three. The bifurcations then begin again with period 6, 12, 24, then back to chaos. In fact it was discovered in James Yorke's famous paper "Period Three Implies Chaos." that any sequence with a period of three will display regular cycles of every other period as well as exhibiting chaotic cycles.
The bifurcation diagram of the logistic difference equation is shown below: